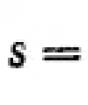Aritmetik ilerlemenin toplamı. Sonlu bir aritmetik ilerlemenin terimlerinin toplamı formülü, fonksiyonlara ve türevlere aşina hale gelebilir

SAYISAL DİZİLER VI

§ 144. Aritmetik ilerlemenin terimlerinin toplamı

Sınıfı uzun süre bağımsız çalışmalarla meşgul etmek isteyen bir ilkokul öğretmeninin, bir gün çocuklara 1'den 100'e kadar tüm doğal sayıların toplamını hesaplamak için "zor" bir görev verdiğini söylüyorlar:

1 + 2 + 3 + 4 + ... + 100.

Öğrencilerden biri hemen bir çözüm önerdi. İşte burada.:

1+2 +3+... + 98 +99+ 100 = (1 + 100) + (2 + 99) + (3 + 98) + ... +(49 + 52)+ (50 + 51) =
= 101 + 101 + . . . + 101 + 101 = 101 50 = 5050.
50 kere

Bu kişi, daha sonra dünyanın en ünlü matematikçilerinden biri olacak olan Carl Gauss'du*.

*Gauss'ta da benzer bir durum yaşandı. Ancak burada büyük ölçüde basitleştirilmiştir. Öğretmenin önerdiği sayılar beş basamaklıydı ve üç basamaklı farkla aritmetik dizi oluşturuyordu.

Böyle bir çözüm fikri, herhangi bir aritmetik ilerlemenin terimlerinin toplamını bulmak için kullanılabilir.

Lemma. Sonlu bir aritmetik ilerlemenin uçlardan eşit uzaklıktaki iki teriminin toplamı, uç terimlerin toplamına eşittir.

Örneğin sonlu bir aritmetik ilerlemede

1, 2, 3.....98, 99, 100

2 ve 99, 3 ve 98, 4 ve 97 vb. terimler bu ilerlemenin uçlarından eşit uzaklıktadır. Dolayısıyla 2 + 99, 3 + 98, 4 + 97'nin toplamları 1 + 100 uç terimlerinin toplamına eşittir.

Lemmanın kanıtı. Sonlu aritmetik ilerlemeye izin ver

A 1 , A 2 , ..., A N - 1 , A N

herhangi iki üye uçlardan eşit derecede uzaktadır. Diyelim ki bunlardan biri k soldaki terim, yani A k , ve diğer - k sağdaki inci terim, yani A N -k+ 1. Daha sonra

A k + A N -k+ 1 =[A 1 + (k - 1)D ] + [A 1 + (p-k )D ] = 2A 1 + (N - 1)D .

Bu ilerlemenin ekstrem terimlerinin toplamı şuna eşittir:

A 1 + A N = A 1 + [A 1 + (N - 1)D ] = 2A 1 + (N - 1)D .

Böylece,

A k + A N -k+ 1 = A 1 + A N

Q.E.D.

Kanıtlanmış lemmayı kullanarak toplam için genel bir formül elde etmek kolaydır P herhangi bir aritmetik ilerlemenin üyeleri.

S N = A 1 +A 2 + ...+ A N - 1 + A N

S N = A N + A N - 1 + ... + A 2 + A 1 .

Bu iki eşitliği terim terim topladığımızda şunu elde ederiz:

2S N = (A 1 +A N ) + (A 2 +A N - 1)+...+(A N - 1 +A 2) + (A N +A 1)

A 1 +A N = A 2 +A N - 1 = A 3 +A N - 2 =... .

2S N = N (A 1 +A N ),

Sonlu bir aritmetik ilerlemenin terimlerinin toplamı, uç terimlerin toplamının yarısı ile tüm terimlerin sayısının çarpımına eşittir.

Özellikle,

Egzersizler

971. Üç basamaklı tüm tek sayıların toplamını bulun.

972. Bir saat yalnızca tam saatlerin sayısını çalarsa gün içinde kaç vuruş yapar?

973. İlkinin toplamı nedir P doğal sayılar mı?

974. Düzgün ivmeli hareket sırasında bir cismin kat ettiği yolun uzunluğu için formülü türetin:

Nerede v 0 - başlangıç ​​hızı m/sn , A - hızlanma m/sn 2 , T - seyahat süresi saniye.

975. Pozitif tamsayılar arasında paydası 3 olan tüm indirgenemez kesirlerin toplamını bulun T Ve P (T< п ).

976. Bir işçi 16 otomatik dokuma tezgâhının bakımını yapıyor. Her makinenin verimliliği A m/sa. İşçi ilk makineyi saat 7'de açtı H ve sonraki her biri 5'er dk.öncekinden daha geç. İlk 2'nin üretimini metre cinsinden öğrenin H iş.

977. Denklemleri çözün:

a) 1 + 7 + 13 + ... + X = 280;

B) ( X + 1) + (X + 4) + (X + 7) +...+ (X + 28) = 155

978. 1 Temmuz'dan 12 Temmuz'a kadar hava sıcaklığı her gün ortalama 1/2 derece arttı. Bu süre zarfında ortalama sıcaklığın 18 3/4 derece olduğunu bilerek, 1 Temmuz'da hava sıcaklığının ne olduğunu belirleyin.

979. Aritmetik ortalaması şu şekilde olan bir aritmetik ilerleme bulun: P herhangi biri için ilk koşullar P sayılarına eşittir.

980. Aritmetik ilerlemenin ilk yirmi teriminin toplamını bulun.

A 6 + A 9 + A 12 + A 15 = 20.

Aritmetik ilerlemenin toplamı.

Aritmetik ilerlemenin toplamı basit bir şeydir. Hem anlam hem de formül olarak. Ancak bu konuyla ilgili her türlü görev var. Temelden oldukça sağlama.

Öncelikle miktarın anlamını ve formülünü anlayalım. Ve sonra karar vereceğiz. Kendi zevkiniz için.) Miktarın anlamı möö kadar basittir. Aritmetik ilerlemenin toplamını bulmak için tüm terimlerini dikkatlice eklemeniz yeterlidir. Bu terimler azsa formül kullanmadan ekleyebilirsiniz. Ama çok ya da çok varsa... ekleme can sıkıcıdır.) Bu durumda formül imdadımıza yetişir.

Miktarın formülü basittir:

Formülde ne tür harflerin yer aldığını bulalım. Bu, işleri büyük ölçüde açıklığa kavuşturacaktır.

Sn - aritmetik ilerlemenin toplamı. Toplama sonucu herkesüyeleri ile Birinciİle son. Bu önemli. Tam olarak topluyorlar Tümüyeleri atlamadan veya atlamadan arka arkaya. Ve tam olarak şundan başlayarak Birinci.Üçüncü ve sekizinci terimlerin toplamını veya beşinci ila yirminci terimlerin toplamını bulma gibi problemlerde formülün doğrudan uygulanması hayal kırıklığı yaratacaktır.)

1 - Birinci ilerlemenin üyesi. Burada her şey açık, çok basit Birinci satır numarası.

BİR- son ilerlemenin üyesi. Serinin son sayısı. Çok tanıdık bir isim değil ama miktara uygulandığında çok uygun. O zaman kendin göreceksin.

N - son üyenin numarası. Formülde bu sayının olduğunu anlamak önemlidir. eklenen terimlerin sayısıyla örtüşür.

Konsepti tanımlayalım sonüye BİR. Zor soru: Hangi üye olacak sonuncu eğer verilirse sonsuz aritmetik ilerleme?)

Kendinize güvenerek cevap verebilmek için aritmetik ilerlemenin temel anlamını anlamanız ve... görevi dikkatlice okumanız gerekir!)

Bir aritmetik ilerlemenin toplamını bulma görevinde her zaman son terim görünür (doğrudan veya dolaylı olarak), ki bu sınırlı olmalıdır. Aksi takdirde, nihai, belirli bir miktar basitçe mevcut değil.Çözüm için ilerlemenin verilip verilmediği önemli değildir: sonlu veya sonsuz. Nasıl verildiği önemli değil: bir dizi sayı ya da n'inci terim için bir formül.

En önemli şey, formülün ilerlemenin ilk döneminden sayı içeren döneme kadar çalıştığını anlamaktır. N. Aslında formülün tam adı şuna benzer: bir aritmetik ilerlemenin ilk n teriminin toplamı. Bu ilk üyelerin sayısı, yani. N, yalnızca göreve göre belirlenir. Bir görevde, tüm bu değerli bilgiler genellikle şifrelenir, evet... Ama boş verin, aşağıdaki örneklerde bu sırları açığa çıkarıyoruz.)

Aritmetik ilerlemenin toplamı ile ilgili görev örnekleri.

Öncelikle faydalı bilgiler:

Aritmetik ilerlemenin toplamını içeren görevlerdeki temel zorluk, formülün öğelerinin doğru belirlenmesinde yatmaktadır.

Görev yazarları bu unsurları sınırsız hayal gücüyle şifreler.) Burada asıl önemli olan korkmamaktır. Elementlerin özünü anlamak, onları basitçe deşifre etmek yeterlidir. Birkaç örneğe ayrıntılı olarak bakalım. Gerçek bir GIA'ya dayalı bir görevle başlayalım.

1. Aritmetik ilerleme şu koşulla verilir: a n = 2n-3,5. İlk 10 teriminin toplamını bulun.

Aferin. Kolay.) Formülü kullanarak miktarı belirlemek için neyi bilmemiz gerekiyor? İlk üye 1, son dönem BİR, evet son üyenin numarası N.

Son üyenin numarasını nereden alabilirim? N? Evet, şartla orada! Diyor ki: toplamı bul ilk 10 üye. Peki hangi numarayla olacak? son, onuncu üye?) İnanmayacaksınız, numarası onuncu!) Bu nedenle, yerine BİR Formülde yerine koyacağız 10 ve bunun yerine N- on. Tekrar ediyorum, son üye sayısı üye sayısıyla örtüşüyor.

Belirlemek için kalır 1 Ve 10. Bu, problem tanımında verilen n'inci terim formülü kullanılarak kolayca hesaplanır. Bunu nasıl yapacağınızı bilmiyor musunuz? Önceki derse katılın, bu olmadan hiçbir yolu yoktur.

1= 2 1 - 3,5 = -1,5

10=2·10 - 3,5 =16,5

Sn = S10.

Aritmetik ilerlemenin toplamı formülündeki tüm öğelerin anlamını bulduk. Geriye kalan tek şey bunları değiştirmek ve saymaktır:

Bu kadar. Cevap: 75.

GIA'ya dayanan başka bir görev. Biraz daha karmaşık:

2. Farkı 3,7 olan aritmetik ilerleme (a n) verildiğinde; a 1 =2,3. İlk 15 teriminin toplamını bulun.

Hemen toplam formülünü yazıyoruz:

Bu formül herhangi bir terimin değerini numarasına göre bulmamızı sağlar. Basit bir ikame arıyoruz:

15 = 2,3 + (15-1) 3,7 = 54,1

Aritmetik ilerlemenin toplamı için formüldeki tüm unsurları yerine koymak ve cevabı hesaplamak kalır:

Cevap: 423.

Bu arada, eğer toplam formülünde yerine BİR Formülü n'inci terimin yerine koyarız ve şunu elde ederiz:

Benzerlerini sunalım ve bir aritmetik ilerlemenin terimlerinin toplamı için yeni bir formül elde edelim:

Gördüğünüz gibi burada n'inci terime gerek yok BİR. Bazı problemlerde bu formül çok işe yarıyor evet... Bu formülü hatırlarsınız. Veya buradaki gibi doğru zamanda görüntüleyebilirsiniz. Sonuçta, toplamın formülünü ve n'inci terimin formülünü her zaman hatırlamanız gerekir.)

Şimdi görev kısa bir şifreleme şeklinde):

3. Üçün katı olan iki basamaklı tüm pozitif sayıların toplamını bulun.

Vay! Ne ilk üyen, ne son üyen, ne de ilerleyişin… Nasıl yaşanır!?

Kafanızla düşünmeniz ve durumdan aritmetik ilerlemenin toplamının tüm unsurlarını çıkarmanız gerekecek. İki basamaklı sayıların ne olduğunu biliyoruz. İki sayıdan oluşurlar.) İki basamaklı sayı ne olacak? Birinci? 10, muhtemelen.) A son şeyçift ​​haneli sayı mı? 99 elbette! Üç haneli olanlar onu takip edecek...

Üçün katları... Hımm... Bunlar üçe bölünebilen sayılar, işte! On üçe bölünmez, 11 bölünmez... 12... bölünür! Yani bir şeyler ortaya çıkıyor. Sorunun koşullarına göre zaten bir dizi yazabilirsiniz:

12, 15, 18, 21, ... 96, 99.

Bu seri aritmetik bir ilerleme mi olacak? Kesinlikle! Her terim bir öncekinden kesinlikle üç farklılık gösterir. Bir terime 2 veya 4 eklerseniz sonuç; yeni sayı artık 3'e bölünemez. Aritmetik ilerlemenin farkını hemen belirleyebilirsiniz: d = 3.İşinize yarayacaktır!)

Böylece bazı ilerleme parametrelerini güvenle yazabiliriz:

Sayı ne olacak? N son üye? 99'un ölümcül bir yanılgı olduğunu düşünenler... Rakamlar hep arka arkaya gidiyor ama üyelerimiz üçün üzerine atlıyor. Eşleşmiyorlar.

Burada iki çözüm var. Bunun bir yolu süper çalışkanlar içindir. İlerlemeyi, tüm sayı dizisini yazabilir ve üye sayısını parmağınızla sayabilirsiniz.) İkinci yol düşünceli olanlar içindir. N'inci dönemin formülünü hatırlamanız gerekiyor. Formülü problemimize uygularsak 99'un ilerlemenin otuzuncu terimi olduğunu buluruz. Onlar. n = 30.

Aritmetik ilerlemenin toplamının formülüne bakalım:

Bakıyoruz ve seviniyoruz.) Sorun ifadesinden tutarı hesaplamak için gereken her şeyi çıkardık:

1= 12.

30= 99.

Sn = S 30.

Geriye kalan tek şey temel aritmetiktir. Sayıları formülde yerine koyarız ve hesaplarız:

Cevap: 1665

Başka bir popüler bulmaca türü:

4. Aritmetik ilerleme verildiğinde:

-21,5; -20; -18,5; -17; ...

Yirmiden otuz dörde kadar terimlerin toplamını bulun.

Miktarın formülüne bakıyoruz ve... üzülüyoruz.) Formül, hatırlatayım, tutarı hesaplıyor. birincidenüye. Ve problemde toplamı hesaplamanız gerekiyor yirminci yüzyıldan beri... Formül işe yaramayacak.

Elbette tüm ilerlemeyi bir seri halinde yazabilir ve 20'den 34'e kadar terimler ekleyebilirsiniz. Ama... bu bir şekilde aptalca ve uzun zaman alıyor, değil mi?)

Daha zarif bir çözüm var. Serimizi iki parçaya ayıralım. İlk bölüm olacak ilk dönemden on dokuzuncu döneme kadar.İkinci kısım - yirmiden otuz dörde kadar.İlk bölümün terimlerinin toplamını hesaplarsak açıktır ki S 1-19, ikinci bölümün terimlerinin toplamını ekleyelim S 20-34, birinci dönemden otuz dördüncü döneme kadar olan ilerlemenin toplamını elde ederiz S1-34. Bunun gibi:

S 1-19 + S 20-34 = S1-34

Bundan toplamı bulduğumuzu görebiliriz. S 20-34 basit çıkarma işlemiyle yapılabilir

S 20-34 = S1-34 - S 1-19

Sağ taraftaki her iki miktar da dikkate alınır birincidenüye, yani standart toplam formülü onlara oldukça uygulanabilir. Başlayalım?

İlerleme parametrelerini problem ifadesinden çıkarıyoruz:

d = 1,5.

1= -21,5.

İlk 19 ve ilk 34 terimin toplamını hesaplamak için 19. ve 34. terimlere ihtiyacımız olacak. Bunları problem 2'deki gibi n'inci terim formülünü kullanarak hesaplıyoruz:

19= -21,5 +(19-1) 1,5 = 5,5

34= -21,5 +(34-1) 1,5 = 28

Hiçbirşey kalmadı. 34 terimin toplamından 19 terimin toplamını çıkarın:

S 20-34 = S 1-34 - S 1-19 = 110,5 - (-152) = 262,5

Cevap: 262.5

Önemli bir not! Bu sorunu çözmenin çok faydalı bir hilesi var. Doğrudan hesaplama yerine neye ihtiyacınız var (S 20-34), saydık ihtiyaç duyulmayan bir şey - S 1-19. Ve sonra karar verdiler S 20-34 gereksiz olanı sonuçtan çıkararak. Bu tür bir "kulak yanıltması" çoğu zaman sizi kötü sorunlardan kurtarır.)

Bu derste aritmetik ilerlemenin toplamının anlamını anlamanın yeterli olduğu problemlere baktık. Birkaç formül bilmeniz gerekiyor.)

Pratik tavsiye:

Aritmetik ilerlemenin toplamını içeren herhangi bir problemi çözerken, bu konudaki iki ana formülü hemen yazmanızı öneririm.

N'inci terimin formülü:

Bu formüller size sorunu çözmek için neye bakmanız ve hangi yönde düşünmeniz gerektiğini hemen söyleyecektir. Yardım eder.

Ve şimdi bağımsız çözüm için görevler.

5. Üçe bölünemeyen iki basamaklı tüm sayıların toplamını bulun.

Harika mı?) İpucu 4. problemin notunda gizli. Peki, 3. problem yardımcı olacaktır.

6. Aritmetik ilerleme şu koşulla verilir: a 1 = -5,5; a n+1 = a n +0,5. İlk 24 teriminin toplamını bulun.

Olağandışı mı?) Bu yinelenen bir formüldür. Bunu önceki derste okuyabilirsiniz. Bağlantıyı göz ardı etmeyin, bu tür sorunlara Devlet Bilimler Akademisi'nde sıklıkla rastlanır.

7. Vasya tatil için para biriktirdi. 4550 ruble kadar! Ve en sevdiğim kişiye (kendime) birkaç günlük mutluluk vermeye karar verdim). Kendinize hiçbir şeyi inkar etmeden güzel yaşayın. İlk gün 500 ruble harcayın ve sonraki her gün bir öncekinden 50 ruble daha fazla harcayın! Ta ki para bitene kadar. Vasya'nın kaç günü mutluluk vardı?

Zor mu?) 2. problemdeki ek formül yardımcı olacaktır.

Cevaplar (karışıklık içinde): 7, 3240, 6.

Bu siteyi beğendiyseniz...

Bu arada, sizin için birkaç ilginç sitem daha var.)

Örnek çözerek pratik yapabilir ve seviyenizi öğrenebilirsiniz. Anında doğrulama ile test etme. Hadi öğrenelim - ilgiyle!)

Fonksiyonlar ve türevler hakkında bilgi sahibi olabilirsiniz.

Ders türü: yeni materyal öğrenmek.

Dersin Hedefleri:

• öğrencilerin aritmetik ilerleme kullanılarak çözülen problemlere ilişkin anlayışlarını genişletmek ve derinleştirmek; bir aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formülü türetirken öğrencilerin arama etkinliklerini organize etmek;
• bağımsız olarak yeni bilgi edinme ve belirli bir görevi gerçekleştirmek için önceden edinilmiş bilgileri kullanma yeteneğini geliştirmek;
• elde edilen gerçekleri genelleme arzusunu ve ihtiyacını geliştirmek, bağımsızlığı geliştirmek.

Görevler:

• “Aritmetik ilerleme” konusundaki mevcut bilgileri özetlemek ve sistematik hale getirmek;
• bir aritmetik ilerlemenin ilk n teriminin toplamını hesaplamak için formüller türetmek;
• elde edilen formüllerin çeşitli problemleri çözerken nasıl uygulanacağını öğretmek;
• Öğrencilerin dikkatini sayısal bir ifadenin değerini bulma prosedürüne çekin.

Teçhizat:

• gruplar ve çiftler halinde çalışmaya yönelik görevleri içeren kartlar;
• değerlendirme belgesi;
• sunum"Aritmetik ilerleme."

I. Temel bilgilerin güncellenmesi.

1. Çiftler halinde bağımsız çalışma.

1. seçenek:

Aritmetik ilerlemeyi tanımlayın. Aritmetik ilerlemeyi tanımlayan bir yineleme formülü yazın. Lütfen aritmetik ilerlemeye bir örnek verin ve farkını belirtin.

2. seçenek:

Aritmetik ilerlemenin n'inci teriminin formülünü yazın. Aritmetik ilerlemenin 100. terimini bulun ( BİR}: 2, 5, 8 …
Bu sırada tahtanın arkasında oturan iki öğrenci aynı soruların cevaplarını hazırlıyor.
Öğrenciler arkadaşlarının çalışmalarını tahtada kontrol ederek değerlendirirler. (Cevapların bulunduğu kağıtlar teslim edilir.)

2. Oyun anı.

1. Egzersiz.

Öğretmen. Bazı aritmetik ilerlemeler düşündüm. Bana sadece iki soru sor ki cevaplardan sonra bu ilerlemenin 7. dönemini hızlı bir şekilde adlandırabilesin. (1, 3, 5, 7, 9, 11, 13, 15…)

Öğrencilerden gelen sorular.

1. İlerlemenin altıncı dönemi nedir ve fark nedir?
2. İlerlemenin sekizinci terimi nedir ve fark nedir?

Başka soru yoksa, öğretmen onları teşvik edebilir - d'ye (fark) "yasak", yani farkın neye eşit olduğunu sormaya izin verilmez. Soru sorabilirsiniz: ilerlemenin 6. terimi neye eşittir ve ilerlemenin 8. terimi neye eşittir?

Görev 2.

Tahtada yazılı 20 sayı vardır: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

Öğretmen sırtı tahtaya dönük olarak durur. Öğrenciler numarayı söyler ve öğretmen anında numaranın kendisini söyler. Bunu nasıl yapabileceğimi açıkla?

Öğretmen n'inci dönemin formülünü hatırlıyor bir n = 3n – 2 ve belirtilen n değerlerini değiştirerek karşılık gelen değerleri bulur BİR.

II. Bir öğrenme görevi ayarlama.

Mısır papirüslerinde bulunan, MÖ 2. binyıla kadar uzanan eski bir sorunu çözmeyi öneriyorum.

Görev:“Size şunu söyleyelim: 10 ölçek arpayı 10 kişiye bölüştürün, her kişiyle komşusu arasındaki fark 1/8 kadardır.”

• Bu problemin aritmetik ilerleme konusuyla nasıl bir bağlantısı var? (Sonraki her kişi ölçünün 1/8'i kadar fazla alır yani fark d=1/8, 10 kişi yani n=10 olur.)
• Sizce 10 numaralı tedbir ne anlama geliyor? (İlerlemenin tüm terimlerinin toplamı.)
• Arpanın problemin koşullarına göre bölünmesini kolay ve basit hale getirmek için bilmeniz gereken başka neler var? (İlerlemenin ilk dönemi.)

Dersin Amacı– ilerlemenin terimlerinin toplamının sayılarına, ilk terime ve farka bağımlılığını elde etmek ve eski zamanlarda problemin doğru çözülüp çözülmediğini kontrol etmek.

Formülü çıkarmadan önce eski Mısırlıların sorunu nasıl çözdüklerine bakalım.

Ve bunu şu şekilde çözdüler:

1) 10 ölçü: 10 = 1 ölçü – ortalama pay;
2) 1 ölçü ∙ = 2 ölçü – iki katına çıkar ortalama paylaşmak.
İki katına çıktı ortalama hisse 5. ve 6. şahısların hisselerinin toplamıdır.
3) 2 ölçü – 1/8 ölçü = 1 7/8 ölçü – beşinci kişinin payının iki katı.
4) 1 7/8: 2 = 5/16 – beşte bir kesri; vb. her bir önceki ve sonraki kişinin payını bulabilirsiniz.

Sırayı alıyoruz:

III. Sorunu çözmek.

1. Grup halinde çalışın

Grup I: Ardışık 20 doğal sayının toplamını bulun: S 20 =(20+1)∙10 =210.

Genel olarak

II grubu: 1'den 100'e kadar doğal sayıların toplamını bulun (Küçük Gauss Efsanesi).

S 100 = (1+100)∙50 = 5050

Çözüm:

III grubu: 1'den 21'e kadar doğal sayıların toplamını bulun.

Çözüm: 1+21=2+20=3+19=4+18…

Çözüm:

IV grubu: 1'den 101'e kadar doğal sayıların toplamını bulun.

Çözüm:

Ele alınan problemleri çözmenin bu yöntemine “Gauss Yöntemi” denir.

2. Her grup problemin çözümünü tahtada sunar.

3. Keyfi bir aritmetik ilerleme için önerilen çözümlerin genelleştirilmesi:

a 1, a 2, a 3,…, a n-2, a n-1, a n.
S n =a 1 + a 2 + a 3 + a 4 +…+ a n-3 + a n-2 + a n-1 + a n.

Benzer akıl yürütmeyi kullanarak bu toplamı bulalım:

4. Sorunu çözdük mü?(Evet.)

IV. Elde edilen formüllerin problem çözümünde temel olarak anlaşılması ve uygulanması.

1. Formülü kullanarak eski bir problemin çözümünü kontrol etmek.

2. Formülün çeşitli problemlerin çözümünde uygulanması.

3. Problem çözerken formülleri uygulama yeteneğini geliştirmeye yönelik alıştırmalar.

A) 613 Sayılı

Verilen: ( BİR) - aritmetik ilerleme;

(bir n): 1, 2, 3,…, 1500

Bulmak: S 1500

Çözüm: , a 1 = 1 ve 1500 = 1500,

B) Verilen: ( BİR) - aritmetik ilerleme;
(bir n): 1, 2, 3, …
Sn = 210

Bulmak: N
Çözüm:

V. Karşılıklı doğrulama ile bağımsız çalışma.

Denis kurye olarak çalışmaya başladı. İlk ayda maaşı 200 rubleydi, sonraki her ayda ise 30 ruble arttı. Bir yılda toplam ne kadar kazandı?

Verilen: ( BİR) - aritmetik ilerleme;
a 1 = 200, d=30, n=12
Bulmak: S12
Çözüm:

Cevap: Denis yıl için 4380 ruble aldı.

VI. Ev ödevi talimatı.

1. Bölüm 4.3 – formülün türetilmesini öğrenin.
2. №№ 585, 623 .
3. Bir aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formül kullanılarak çözülebilecek bir problem oluşturun.

VII. Dersi özetlemek.

1. Puan Tablosu

2. Cümlelere devam edin

• Bugün sınıfta öğrendim...
• Öğrenilen formüller...
• İnanıyorum ki …

3. 1'den 500'e kadar sayıların toplamını bulabilir misiniz? Bu sorunu çözmek için hangi yöntemi kullanacaksınız?

Kaynakça.

1. Cebir, 9. sınıf. Genel eğitim kurumları için ders kitabı. Ed. G.V. Dorofeeva. M.: “Aydınlanma”, 2009.

Ortaokulda (9. sınıf) cebir çalışırken önemli konulardan biri geometrik ve aritmetik ilerlemeleri içeren sayısal dizilerin incelenmesidir. Bu yazıda aritmetik ilerlemeye ve çözümlü örneklere bakacağız.

Aritmetik ilerleme nedir?

Bunu anlamak için hem söz konusu ilerlemeyi tanımlamak hem de daha sonra problemlerin çözümünde kullanılacak temel formülleri sağlamak gerekir.

Aritmetik veya cebirsel ilerleme, her bir terimi bir öncekinden sabit bir değerle farklı olan bir dizi sıralı rasyonel sayıdır. Bu değere fark denir. Yani, sıralı bir sayı serisinin herhangi bir üyesini ve farkı bilerek, tüm aritmetik ilerlemeyi geri yükleyebilirsiniz.

Bir örnek verelim. Aşağıdaki sayı dizisi aritmetik bir ilerleme olacaktır: 4, 8, 12, 16, ..., çünkü bu durumda fark 4'tür (8 - 4 = 12 - 8 = 16 - 12). Ancak 3, 5, 8, 12, 17 sayıları kümesi artık söz konusu ilerleme türüne atfedilemez, çünkü bunun farkı sabit bir değer değildir (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Önemli Formüller

Şimdi aritmetik ilerlemeyi kullanarak problemleri çözmek için ihtiyaç duyacağımız temel formülleri sunalım. Dizinin n'inci üyesini a n sembolüyle gösterelim; burada n bir tam sayıdır. Farkı Latin harfi d ile belirtiyoruz. O halde aşağıdaki ifadeler geçerlidir:

1. N'inci terimin değerini belirlemek için aşağıdaki formül uygundur: a n = (n-1)*d+a 1 .
2. İlk n terimin toplamını belirlemek için: S n = (a n +a 1)*n/2.

9. sınıftaki çözümlerle ilgili herhangi bir aritmetik ilerleme örneğini anlamak için, bu iki formülü hatırlamak yeterlidir, çünkü söz konusu türdeki herhangi bir problem bunların kullanımına dayanmaktadır. İlerleme farkının şu formülle belirlendiğini de unutmamalısınız: d = a n - a n-1.

Örnek 1: bilinmeyen bir üyeyi bulma

Aritmetik ilerlemeye ve onu çözmek için kullanılması gereken formüllere basit bir örnek verelim.

10, 8, 6, 4, ... dizisi verilsin, içinde beş terim bulmanız gerekiyor.

Problemin koşullarından ilk 4 terimin zaten bilindiği sonucu çıkıyor. Beşincisi iki şekilde tanımlanabilir:

1. Önce farkı hesaplayalım. Elimizde: d = 8 - 10 = -2. Benzer şekilde, yan yana duran diğer iki üyeyi de alabilirsiniz. Örneğin d = 4 - 6 = -2. D = a n - a n-1 olduğu bilindiğinden, d = a 5 - a 4 olur ve bundan şunu elde ederiz: a 5 = a 4 + d. Bilinen değerleri yerine koyarız: a 5 = 4 + (-2) = 2.
2. İkinci yöntem de söz konusu ilerlemenin farkının bilinmesini gerektirir, bu nedenle öncelikle bunu yukarıda gösterildiği gibi belirlemeniz gerekir (d = -2). İlk terimin a 1 = 10 olduğunu bilerek dizinin n sayısı için formülü kullanıyoruz. Elimizde: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2*n. Son ifadede n = 5'i yerine koyarsak şunu elde ederiz: a 5 = 12-2 * 5 = 2.

Gördüğünüz gibi her iki çözüm de aynı sonuca yol açtı. Bu örnekte ilerleme farkı d'nin negatif bir değer olduğuna dikkat edin. Bu tür dizilere azalan diziler denir, çünkü sonraki her terim bir öncekinden daha küçüktür.

Örnek #2: ilerleme farkı

Şimdi görevi biraz karmaşıklaştıralım, nasıl yapıldığına dair bir örnek verelim

Bazılarında 1. terimin 6'ya, 7. terimin ise 18'e eşit olduğu bilinmektedir. Farkı bulup bu diziyi 7. terime geri döndürmek gerekir.

Bilinmeyen terimi belirlemek için şu formülü kullanalım: a n = (n - 1) * d + a 1 . Koşuldan bilinen verileri, yani a 1 ve a 7 sayılarını yerine koyalım: 18 = 6 + 6 * d. Bu ifadeden farkı kolayca hesaplayabilirsiniz: d = (18 - 6) /6 = 2. Böylece problemin ilk kısmını cevaplamış olduk.

Diziyi 7. terime geri döndürmek için cebirsel ilerlemenin tanımını kullanmalısınız, yani a 2 = a 1 + d, a 3 = a 2 + d vb. Sonuç olarak tüm diziyi geri yükleriz: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.

Örnek No. 3: bir ilerlemenin hazırlanması

Sorunu daha da karmaşık hale getirelim. Şimdi aritmetik ilerlemenin nasıl bulunacağı sorusunu cevaplamamız gerekiyor. Şu örneği verebiliriz: İki sayı veriliyor örneğin - 4 ve 5. Bunların arasına üç terim daha yerleştirilecek şekilde cebirsel bir ilerleme oluşturmak gerekiyor.

Bu sorunu çözmeye başlamadan önce, verilen sayıların gelecekteki ilerlemede nasıl bir yer tutacağını anlamalısınız. Aralarında üç terim daha olacağı için a 1 = -4 ve a 5 = 5 olur. Bunu belirledikten sonra bir öncekine benzer probleme geçiyoruz. Yine formülü kullandığımız n'inci terim için şunu elde ederiz: a 5 = a 1 + 4 * d. Başlangıç: d = (a 5 - a 1)/4 = (5 - (-4)) / 4 = 2,25. Burada elde ettiğimiz şey farkın tam sayı değeri değil, rasyonel bir sayıdır, dolayısıyla cebirsel ilerlemenin formülleri aynı kalır.

Şimdi bulunan farkı 1'e ekleyelim ve ilerlemenin eksik terimlerini geri yükleyelim. Şunu elde ederiz: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 = 2,75 + 2,25 = 5, bunlar çakıştı Sorunun koşulları ile.

Örnek No. 4: ilerlemenin ilk dönemi

Çözümlü aritmetik ilerleme örnekleri vermeye devam edelim. Önceki problemlerin hepsinde cebirsel ilerlemenin ilk sayısı biliniyordu. Şimdi farklı türde bir problem düşünelim: a 15 = 50 ve a 43 = 37 olmak üzere iki sayı verilsin. Bu dizinin hangi sayıyla başladığını bulmak gerekiyor.

Şu ana kadar kullanılan formüller a 1 ve d'nin bilgisini varsaymaktadır. Problem ifadesinde bu sayılar hakkında hiçbir şey bilinmemektedir. Bununla birlikte, hakkında bilgi bulunan her terim için ifadeleri yazacağız: a 15 = a 1 + 14 * d ve a 43 = a 1 + 42 * d. 2 bilinmeyen miktarın (a 1 ve d) olduğu iki denklem aldık. Bu, problemin bir doğrusal denklem sisteminin çözümüne indirgendiği anlamına gelir.

Bu sistemi çözmenin en kolay yolu, her denklemde 1'i ifade etmek ve ardından elde edilen ifadeleri karşılaştırmaktır. Birinci denklem: a 1 = a 15 - 14 * d = 50 - 14 * d; ikinci denklem: a 1 = a 43 - 42 * d = 37 - 42 * d. Bu ifadeleri eşitleyerek şunu elde ederiz: 50 - 14 * d = 37 - 42 * d, dolayısıyla fark d = (37 - 50) / (42 - 14) = - 0,464 (sadece 3 ondalık basamak verilmiştir).

D'yi bildiğinize göre, 1 için yukarıdaki 2 ifadeden herhangi birini kullanabilirsiniz. Örneğin ilk olarak: a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.

Elde edilen sonuçtan şüpheniz varsa kontrol edebilirsiniz, örneğin durumda belirtilen ilerlemenin 43. dönemini belirleyebilirsiniz. Şunu elde ederiz: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Küçük hata, hesaplamalarda binde birine yuvarlamanın kullanılmasından kaynaklanmaktadır.

Örnek No. 5: tutar

Şimdi bir aritmetik ilerlemenin toplamının çözümlerini içeren birkaç örneğe bakalım.

Aşağıdaki formun sayısal ilerlemesi verilsin: 1, 2, 3, 4, ...,. Bu sayıların 100'ünün toplamı nasıl hesaplanır?

Bilgisayar teknolojisinin gelişmesi sayesinde bu sorunu çözmek, yani tüm sayıları sırayla eklemek mümkündür; kişi Enter tuşuna bastığı anda bilgisayar bunu yapar. Ancak sunulan sayı serisinin cebirsel bir ilerleme olduğuna ve farkının 1'e eşit olduğuna dikkat ederseniz sorun zihinsel olarak çözülebilir. Toplam formülünü uygulayarak şunu elde ederiz: S n = n * (a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.

Bu problemin “Gaussian” olarak adlandırılması ilginçtir çünkü 18. yüzyılın başında, henüz 10 yaşında olan ünlü Alman, bu problemi birkaç saniye içinde kafasında çözebilmiştir. Çocuk cebirsel ilerlemenin toplamının formülünü bilmiyordu ama dizinin sonundaki sayıları çiftler halinde toplarsanız her zaman aynı sonucu elde ettiğinizi fark etti: 1 + 100 = 2 + 99 = 3 + 98 = ... ve bu toplamlar tam olarak 50 (100/2) olacağından doğru cevabı almak için 50'yi 101 ile çarpmak yeterlidir.

Örnek No. 6: n'den m'ye kadar terimlerin toplamı

Aritmetik ilerlemenin toplamının bir başka tipik örneği şudur: 3, 7, 11, 15, ... gibi bir sayı dizisi verildiğinde, 8'den 14'e kadar olan terimlerin toplamının neye eşit olacağını bulmanız gerekir. .

Sorun iki şekilde çözülür. Bunlardan ilki, 8'den 14'e kadar bilinmeyen terimleri bulmayı ve ardından bunları sırayla toplamayı içerir. Terim sayısı az olduğundan bu yöntem pek emek yoğun değildir. Ancak bu sorunun daha evrensel olan ikinci bir yöntemle çözülmesi önerilmektedir.

Buradaki fikir, n > m'nin tamsayı olduğu m ve n terimleri arasındaki cebirsel ilerlemenin toplamı için bir formül elde etmektir. Her iki durumda da toplam için iki ifade yazıyoruz:

1. S m = m * (bir m + bir 1) / 2.
2. S n = n * (bir n + bir 1) / 2.

n > m olduğundan 2. toplamın birinciyi içerdiği açıktır. Son sonuç, bu toplamlar arasındaki farkı alıp buna a m terimini eklersek (farkın alınması durumunda S n toplamından çıkarılırsa) probleme gerekli cevabı elde edeceğimiz anlamına gelir. Elimizde: S mn = S n - S m + a m =n * (a 1 + a n) / 2 - m *(a 1 + a m)/2 + a m = a 1 * (n - m) / 2 + a n * n/2 + a m * (1- m/2). Bu ifadede a n ve a m formüllerini yerine koymak gerekir. O zaman şunu elde ederiz: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d *(3 * m - m 2 - 2) / 2.

Ortaya çıkan formül biraz hantaldır, ancak S mn toplamı yalnızca n, m, a 1 ve d'ye bağlıdır. Bizim durumumuzda a 1 = 3, d = 4, n = 14, m = 8. Bu sayıları yerine koyarsak şunu elde ederiz: S mn = 301.

Yukarıdaki çözümlerden de görülebileceği gibi, tüm problemler n'inci terimin ifadesi ve ilk terimler kümesinin toplamı formülü bilgisine dayanmaktadır. Bu sorunlardan herhangi birini çözmeye başlamadan önce, durumu dikkatlice okumanız, neyi bulmanız gerektiğini net bir şekilde anlamanız ve ancak bundan sonra çözüme devam etmeniz önerilir.

Başka bir ipucu da basitlik için çabalamaktır, yani bir soruyu karmaşık matematiksel hesaplamalar kullanmadan cevaplayabiliyorsanız, o zaman tam da bunu yapmanız gerekir, çünkü bu durumda hata yapma olasılığı daha azdır. Örneğin, 6 numaralı çözümle aritmetik ilerleme örneğinde, S mn = n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m formülünde durabiliriz ve genel problemi ayrı alt görevlere bölün (bu durumda önce a n ve a m terimlerini bulun).

Elde edilen sonuç hakkında şüpheleriniz varsa, verilen bazı örneklerde yapıldığı gibi kontrol etmeniz önerilir. Aritmetik ilerlemeyi nasıl bulacağımızı öğrendik. Bunu anlarsanız, o kadar da zor değil.

Bu derste sonlu bir aritmetik ilerlemenin terimlerinin toplamı için bir formül türeteceğiz ve bu formülü kullanarak bazı problemleri çözeceğiz.

Konu: İlerlemeler

Ders: Sonlu bir aritmetik ilerlemenin terimlerinin toplamı formülü

1. Giriş

Sorunu düşünün: 1'den 100'e kadar olan doğal sayıların toplamını bulun.

Verilenler: 1, 2, 3, …, 98, 99, 100.

Bulunan: S100=1+2+3 … +98 + 99 + 100.

Çözüm: S100=(1+100)+(2+99)+(3+98)+…+(50+51)=101+101+101+…+101=101 x 50=5050.

Cevap: 5050.

1, 2, 3, …, 98, 99, 100 doğal sayıları dizisi aritmetik ilerleme: a1=1, d=1.

İlk yüz doğal sayının toplamını yani ilk n'nin toplamını bulduk. aritmetik ilerleme terimleri.

Düşünülen çözüm, 19. yüzyılda yaşayan büyük matematikçi Carl Friedrich Gauss tarafından önerildi. Sorunu 5 yaşındayken çözdü.

Tarihsel referans: Johann Carl Friedrich Gauss (1777 – 1855) Alman matematikçi, tamirci, fizikçi ve astronomdu. Tüm zamanların en büyük matematikçilerinden biri olarak kabul edilen "Matematikçilerin Kralı". Copley Madalyası (1838) ödüllü, İsveç (1821) ve Rus (1824) Bilim Akademileri ve İngiliz Kraliyet Cemiyeti'nin yabancı üyesi. Efsaneye göre bir okul matematik öğretmeni, çocukları uzun süre oyalamak için onlardan 1'den 100'e kadar olan sayıların toplamını saymalarını istemiştir. Young Gauss zıtlıkların ikili toplamlarının aynı olduğunu fark etmiştir: 1+100=101 , 2+99=101 vb. ve anında şu sonucu elde ettim: 101x50=5050.

2. Aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formülün türetilmesi

Keyfi bir aritmetik ilerleme için benzer bir problemi ele alalım.

Bulduğunuz: bir aritmetik ilerlemenin ilk n teriminin toplamı.

Parantez içindeki tüm ifadelerin birbirine yani ifadeye eşit olduğunu gösterelim. Aritmetik ilerlemenin farkı d olsun. Daha sonra:

Vb. Bu nedenle şunu yazabiliriz:

Bir aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formülü nereden buluruz:

.

3. Aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formülü kullanarak problemleri çözme

1. Bir aritmetik ilerlemenin ilk n teriminin toplamına ilişkin formülü kullanarak 1'den 100'e kadar doğal sayıların toplamı problemini çözelim:

Çözüm: a1=1, d=1, n=100.

Genel formül:

.

Bizim durumumuzda: .

Cevap: 5050.

Genel formül:

. Aşağıdaki formülü kullanarak aritmetik ilerlemenin n'inci terimini bulalım: .

Bizim durumumuzda: .

Bulmak için önce bulmalısınız.

Bu genel formül kullanılarak yapılabilir. .Öncelikle bir aritmetik ilerlemenin farkını bulmak için bu formülü uyguluyoruz.

Yani . Araç .

Artık bulabiliriz.

Bir aritmetik ilerlemenin ilk n teriminin toplamı için formülü kullanma

, bulacağız.

4. Bir aritmetik ilerlemenin ilk n teriminin toplamı için ikinci formülün türetilmesi

Bir aritmetik ilerlemenin ilk n teriminin toplamı için ikinci formülü elde edelim: .

Kanıt:

Bir aritmetik ilerlemenin ilk n teriminin toplamı formülünde ifadesini yerine koyalım, yani . Şunu elde ederiz: , yani. . Q.E.D.

Ortaya çıkan formülleri analiz edelim. İlk formülü kullanan hesaplamalar için ikinci formülü kullanarak ilk terimi, son terimi ve n'yi bilmeniz gerekir - ilk terimi, farkı ve n'yi bilmeniz gerekir.

Ve sonuç olarak, her durumda Sn'nin n'nin ikinci dereceden bir fonksiyonu olduğunu not ediyoruz, çünkü .

5. Aritmetik ilerlemenin ilk n teriminin toplamı için ikinci formülü kullanarak problemleri çözme

Genel formül:

.

Bizim durumumuzda:.

Cevap: 403.

2. 4'ün katı olan tüm iki basamaklı sayıların toplamını bulun.

(12; 16; 20; …; 96) - problemin koşullarını karşılayan bir dizi sayı.

Bu, aritmetik bir ilerlememiz olduğu anlamına gelir.

n'yi aşağıdaki formülden buluyoruz:.

Yani . Araç .

Bir aritmetik ilerlemenin ilk n teriminin toplamı için ikinci formülü kullanma

, bulacağız.

10'uncudan 25'e kadar tüm terimlerin toplamını bulmanız gerekiyor.

Bir çözüm şudur:

Buradan, .

6. Ders özeti

Böylece, sonlu bir aritmetik ilerlemenin terimlerinin toplamı için formüller türetmiş olduk. Bazı problemleri çözmek için bu formülleri kullandık.

Bir sonraki derste aritmetik ilerlemenin karakteristik özelliğini tanıyacağız.

1. Makarychev Yu.N. ve diğerleri Cebir 9. sınıf (lise ders kitabı) - M .: Eğitim, 1992.

2. Makarychev Yu.N., Mindyuk N. G., Neshkov, K. I. İleri düzey 9. sınıf için cebir. okudu Matematik.-M.: Mnemosyne, 2003.

3. Makarychev Yu.N., Mindyuk N. G. 9. sınıf cebir okulu ders kitabı için ek bölümler - M.: Prosveshchenie, 2002.

4. Galitsky M. L., Goldman A. M., Zvavich L. I. 8-9. Sınıflar için cebir problemlerinin toplanması (derinlemesine matematik çalışması olan okul ve sınıf öğrencileri için ders kitabı) - M .: Prosveshchenie, 1996.

5. Mordkovich A.G. Cebir 9. sınıf, genel eğitim kurumları için ders kitabı. - M.: Mnemosyne, 2002.

6. Mordkovich A.G., Mishutina T.N., Tulchinskaya E.E. Cebir 9. sınıf, eğitim kurumları için problem kitabı. - M.: Mnemosyne, 2002.

7. Glazer G.I. Okulda matematik tarihi. 7-8. Sınıflar (öğretmen el kitabı) - M.: Eğitim, 1983.

1. Üniversite bölümü. matematikte ru.

2. Doğa Bilimleri Portalı.

3. Üs. ru Eğitimsel matematik sitesi.

1. No. 362, 371, 377, 382 (Makarychev Yu. N. ve diğerleri. Cebir 9. sınıf).

2. No. 12.96 (Galitsky M.L., Goldman A.M., Zvavich L.I. 8-9. Sınıflar için cebir problemlerinin toplanması).