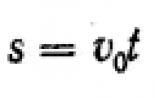Suma unei progresii aritmetice. Formula pentru suma termenilor unei progresii aritmetice finite se poate familiariza cu funcțiile și derivatele
SECVENȚE NUMERICE VI
§ 144. Suma termenilor unei progresii aritmetice
Ei spun că într-o zi un profesor de școală elementară, dorind să țină clasa ocupată cu munca independentă pentru o lungă perioadă de timp, le-a dat copiilor o sarcină „dificilă” - să calculeze suma tuturor numerelor naturale de la 1 la 100:
1 + 2 + 3 + 4 + ... + 100.
Unul dintre elevi a sugerat imediat o soluție. Iată-l.:
1+2 +3+... + 98 +99+ 100 = (1 + 100) + (2 + 99) + (3 + 98) + ... +(49 + 52)+ (50 + 51) =
= 101 + 101 + . . . + 101 + 101
= 101 50 = 5050.
de 50 de ori
Acesta a fost Carl Gauss, care a devenit ulterior unul dintre cei mai faimoși matematicieni din lume*.
*Un caz similar cu Gauss sa întâmplat de fapt. Totuși, aici este foarte simplificat. Numerele propuse de profesor erau de cinci cifre și formau o progresie aritmetică cu o diferență de trei cifre.
Ideea unei astfel de soluții poate fi folosită pentru a găsi suma termenilor oricărei progresii aritmetice.
Lema. Suma a doi termeni ai unei progresii aritmetice finite, echidistante de capete, este egală cu suma termenilor extremi.
De exemplu, într-o progresie aritmetică finită
1, 2, 3.....98, 99, 100
termenii 2 și 99, 3 și 98, 4 și 97 etc. sunt echidistante de capetele acestei progresii. Prin urmare, sumele lor 2 + 99, 3 + 98, 4 + 97 sunt egale cu suma termenilor extremi 1 + 100.
Dovada lemei. Lăsați în progresia aritmetică finită
A 1 , A 2 , ..., A n - 1 , A n
oricare doi membri sunt la fel de îndepărtați de capete. Să presupunem că unul dintre ei este k al treilea termen din stânga, adică A k , si celalalt - k al treilea termen din dreapta, adică A n -k+ 1 . Apoi
A k + A n -k+ 1 =[A 1 + (k - 1)d ] + [A 1 + (p - k )d ] = 2A 1 + (n - 1)d .
Suma termenilor extremi ai acestei progresii este egală cu
A 1 + A n = A 1 + [A 1 + (n - 1)d ] = 2A 1 + (n - 1)d .
Prin urmare,
A k + A n -k+ 1 = A 1 + A n
Q.E.D.
Folosind lema dovedită, este ușor să obțineți o formulă generală pentru suma P membri ai oricărei progresii aritmetice.
S n = A 1 +A 2 + ...+ A n - 1 + A n
S n = A n + A n - 1 + ... + A 2 + A 1 .
Adăugând aceste două egalități termen cu termen, obținem:
2S n = (A 1 +A n ) + (A 2 +A n - 1)+...+(A n - 1 +A 2) + (A n +A 1)
A 1 +A n = A 2 +A n - 1 = A 3 +A n - 2 =... .
2S n = n (A 1 +A n ),
Suma termenilor unei progresii aritmetice finite este egală cu produsul dintre jumătate din suma termenilor extremi și numărul tuturor termenilor.
În special,
Exerciții
971. Aflați suma tuturor numerelor impare din trei cifre.
972. Câte sunete va da un ceas în timpul zilei dacă sună doar numărul de ore întregi?
973. Care este suma primelor P numere de numere naturale?
974. Deduceți formula pentru lungimea drumului parcurs de un corp în timpul mișcării uniform accelerate:
![]()
Unde v 0 - viteza initiala in m/sec , A - accelerație în m/sec 2 , t - timpul de călătorie în sec.
975. Aflați suma tuturor fracțiilor ireductibile cu numitorul 3 între numere întregi pozitive T Și P (T< п ).
976. Un muncitor întreține 16 războaie automate. Productivitatea fiecărei mașini A m/h. Muncitorul a pornit prima mașină la ora 7 h, și fiecare următor câte 5 min mai târziu decât precedentul. Aflați producția în metri pentru primii 2 h muncă.
977. Rezolvați ecuații:
a) 1 + 7 + 13 + ... + X = 280;
b) ( X + 1) + (X + 4) + (X + 7) +...+ (X + 28) = 155
978. De la 1 iulie până la 12 iulie inclusiv, temperatura aerului a crescut zilnic cu o medie de 1/2 grad. Știind că temperatura medie în acest timp s-a dovedit a fi de 18 3/4 de grade, stabiliți care era temperatura aerului la 1 iulie.
979. Găsiți o progresie aritmetică a cărei medie aritmetică este P primii termeni pentru oricare P egală cu numărul lor.
980. Aflați suma primilor douăzeci de termeni ai progresiei aritmetice în care
A 6 + A 9 + A 12 + A 15 = 20.
Suma unei progresii aritmetice.
Suma unei progresii aritmetice este un lucru simplu. Atât în sens, cât și în formulă. Dar există tot felul de sarcini pe această temă. De la bază la destul de solidă.
În primul rând, să înțelegem sensul și formula sumei. Și atunci vom decide. Pentru plăcerea ta.) Sensul sumei este la fel de simplu ca un moo. Pentru a găsi suma unei progresii aritmetice, trebuie doar să adăugați cu atenție toți termenii acesteia. Dacă acești termeni sunt puțini, puteți adăuga fără formule. Dar dacă există mult, sau mult... adaosul este enervant.) În acest caz, formula vine în ajutor.
Formula pentru suma este simplă:
Să ne dăm seama ce fel de litere sunt incluse în formulă. Acest lucru va clarifica foarte mult lucrurile.
S n - suma unei progresii aritmetice. Rezultat adaos toata lumea membri, cu primul De ultimul. Este important. Se adună exact Toate membri la rând, fără săriți sau săriți. Și, tocmai, pornind de la primul.În probleme precum găsirea sumei termenilor al treilea și al optulea sau a sumei termenilor cinci și al douăzecilea, aplicarea directă a formulei va dezamăgi.)
a 1 - primul membru al progresiei. Totul este clar aici, e simplu primul numărul rândului.
un n- ultimul membru al progresiei. Ultimul număr al seriei. Nu este un nume foarte familiar, dar atunci când este aplicat sumei, este foarte potrivit. Atunci vei vedea singur.
n - numărul ultimului membru. Este important să înțelegeți că în formulă acest număr coincide cu numărul de termeni adăugați.
Să definim conceptul ultimul membru un n. Întrebare dificilă: care membru va fi ultimul dacă este dat fără sfârşit progresie aritmetică?)
Pentru a răspunde cu încredere, trebuie să înțelegeți semnificația elementară a progresiei aritmetice și... citiți cu atenție sarcina!)
În sarcina de a găsi suma unei progresii aritmetice, ultimul termen apare întotdeauna (direct sau indirect), care ar trebui limitată.În caz contrar, o sumă finală, specifică pur si simplu nu exista. Pentru soluție, nu contează dacă progresia este dată: finită sau infinită. Nu contează cum este dat: o serie de numere sau o formulă pentru al n-lea termen.
Cel mai important este să înțelegeți că formula funcționează de la primul termen al progresiei până la termenul cu număr n. De fapt, numele complet al formulei arată astfel: suma primilor n termeni ai unei progresii aritmetice. Numărul acestor primi membri, adică n, este determinată exclusiv de sarcină. Într-o sarcină, toate aceste informații valoroase sunt adesea criptate, da... Dar nu contează, în exemplele de mai jos dezvăluim aceste secrete.)
Exemple de sarcini pe suma unei progresii aritmetice.
In primul rand informatii utile:
Principala dificultate în sarcinile care implică suma unei progresii aritmetice constă în determinarea corectă a elementelor formulei.
Scriitorii de sarcini criptează chiar aceste elemente cu o imaginație nemărginită.) Principalul lucru aici este să nu-ți fie frică. Înțelegând esența elementelor, este suficient să le descifrezi pur și simplu. Să ne uităm la câteva exemple în detaliu. Să începem cu o sarcină bazată pe un GIA real.
1. Progresia aritmetică este dată de condiția: a n = 2n-3.5. Aflați suma primilor săi 10 termeni.
Loc de muncă bun. Ușor.) Pentru a determina cantitatea folosind formula, ce trebuie să știm? Primul membru a 1, ultimul termen un n, da numărul ultimului membru n.
De unde pot obține numărul ultimului membru? n? Da, chiar acolo, cu condiție! Se spune: găsiți suma primii 10 membri. Ei bine, cu ce număr va fi? ultimul, al zecelea membru?) Nu veți crede, numărul lui este al zecelea!) Prin urmare, în loc de un n Vom înlocui în formulă un 10, Și în schimb n- zece. Repet, numărul ultimului membru coincide cu numărul membrilor.
Rămâne de stabilit a 1Și un 10. Acest lucru este ușor de calculat folosind formula pentru al n-lea termen, care este dată în enunțul problemei. Nu știi cum să faci asta? Participați la lecția anterioară, fără aceasta nu există nicio cale.
a 1= 2 1 - 3,5 = -1,5
un 10=2·10 - 3,5 =16,5
S n = S 10.
Am aflat semnificația tuturor elementelor formulei pentru suma unei progresii aritmetice. Tot ce rămâne este să le înlocuiți și să numărați:
![]()
Asta este. Raspuns: 75.
O altă sarcină bazată pe GIA. Puțin mai complicat:
2. Având în vedere o progresie aritmetică (a n), a cărei diferență este 3,7; a 1 =2,3. Aflați suma primilor 15 termeni ai săi.
Scriem imediat formula sumei:
Această formulă ne permite să găsim valoarea oricărui termen după numărul său. Căutăm o înlocuire simplă:
a 15 = 2,3 + (15-1) 3,7 = 54,1
Rămâne să înlocuiți toate elementele în formula pentru suma unei progresii aritmetice și să calculați răspunsul:
![]()
Răspuns: 423.
Apropo, dacă în formula sumei în loc de un n Pur și simplu înlocuim formula pentru al n-lea termen și obținem:
Să prezentăm altele similare și să obținem o nouă formulă pentru suma termenilor unei progresii aritmetice:
După cum puteți vedea, al n-lea termen nu este necesar aici un n. În unele probleme această formulă ajută foarte mult, da... Vă puteți aminti această formulă. Sau pur și simplu îl puteți afișa la momentul potrivit, ca aici. La urma urmei, trebuie să vă amintiți întotdeauna formula pentru sumă și formula pentru al n-lea termen.)
Acum sarcina sub forma unei criptări scurte):
3. Aflați suma tuturor numerelor pozitive din două cifre care sunt multipli de trei.
Wow! Nici primul tău membru, nici ultimul, nici progresia deloc... Cum să trăiești!?
Va trebui să gândești cu capul și să scoți toate elementele sumei progresiei aritmetice din condiție. Știm ce sunt numerele din două cifre. Sunt formate din două numere.) Ce număr de două cifre va fi primul? 10, probabil.) A ultimul lucru număr cu două cifre? 99, desigur! Cei din trei cifre îl vor urma...
Multipli de trei... Hm... Acestea sunt numere care sunt divizibile cu trei, aici! Zece nu este divizibil cu trei, 11 nu este divizibil... 12... este divizibil! Deci, ceva iese la iveală. Puteți nota deja o serie în funcție de condițiile problemei:
12, 15, 18, 21, ... 96, 99.
Va fi această serie o progresie aritmetică? Cu siguranță! Fiecare termen diferă de cel precedent prin strict trei. Dacă adăugați 2 sau 4 la un termen, să zicem rezultatul, adică. noul număr nu mai este divizibil cu 3. Puteți determina imediat diferența progresiei aritmetice: d = 3. Asta o să ne mai folosească!)
Deci, putem nota în siguranță câțiva parametri de progresie:
Care va fi numărul? n ultimul membru? Oricine crede că 99 se înșală fatal... Numerele merg mereu la rând, dar membrii noștri sar peste trei. Nu se potrivesc.
Există două soluții aici. O modalitate este pentru cei super muncitori. Puteți nota progresia, întreaga serie de numere și puteți număra numărul de membri cu degetul.) A doua cale este pentru cei gânditori. Trebuie să vă amintiți formula pentru al n-lea termen. Dacă aplicăm formula problemei noastre, aflăm că 99 este al treizecilea termen al progresiei. Acestea. n = 30.
Să ne uităm la formula pentru suma unei progresii aritmetice:
Ne uităm și ne bucurăm.) Am scos din enunțul problemei tot ceea ce era necesar pentru a calcula suma:
a 1= 12.
un 30= 99.
S n = S 30.
Tot ce rămâne este aritmetica elementară. Înlocuim numerele în formulă și calculăm:
![]()
Răspuns: 1665
Un alt tip de puzzle popular:
4. Având în vedere o progresie aritmetică:
-21,5; -20; -18,5; -17; ...
Aflați suma termenilor de la al douăzecilea la treizeci și patru.
Ne uităm la formula pentru suma și... ne supărăm.) Formula, să vă reamintesc, calculează suma din prima membru. Și în problemă trebuie să calculați suma din al XX-lea... Formula nu va funcționa.
Puteți, desigur, să scrieți întreaga progresie într-o serie și să adăugați termeni de la 20 la 34. Dar... este cumva stupid și durează mult, nu?)
Există o soluție mai elegantă. Să împărțim seria noastră în două părți. Prima parte va fi de la primul termen până la al nouăsprezecelea. A doua parte - de la douăzeci la treizeci şi patru. Este clar că dacă calculăm suma termenilor primei părți S 1-19, să-l adunăm cu suma termenilor din partea a doua S 20-34, obținem suma progresiei de la primul termen la al treizeci și patrulea S 1-34. Ca aceasta:
S 1-19 + S 20-34 = S 1-34
Din aceasta putem vedea că găsim suma S 20-34 se poate face prin simpla scădere
S 20-34 = S 1-34 - S 1-19
Sunt luate în considerare ambele sume din partea dreaptă din prima membru, adică formula sumei standard le este destul de aplicabilă. Să începem?
Extragem parametrii de progresie din enunțul problemei:
d = 1,5.
a 1= -21,5.
Pentru a calcula sumele primilor 19 și primilor 34 de termeni, vom avea nevoie de al 19-lea și al 34-lea termen. Le calculăm folosind formula pentru al n-lea termen, ca în problema 2:
un 19= -21,5 +(19-1) 1,5 = 5,5
un 34= -21,5 +(34-1) 1,5 = 28
![]()
Nu a mai rămas nimic. Din suma a 34 de termeni scade suma a 19 termeni:
S 20-34 = S 1-34 - S 1-19 = 110,5 - (-152) = 262,5
Răspuns: 262,5
O notă importantă! Există un truc foarte util în rezolvarea acestei probleme. În loc de calcul direct de ce ai nevoie (S 20-34), am numărat ceva ce ar părea că nu este nevoie - S 1-19.Și atunci s-au hotărât S 20-34, eliminând ceea ce nu este necesar din rezultatul complet. Acest tip de „făcătură cu urechile tale” te salvează adesea în probleme rele.)
În această lecție ne-am uitat la probleme pentru care este suficient să înțelegem sensul sumei unei progresii aritmetice. Ei bine, trebuie să știți câteva formule.)
Sfaturi practice:
Când rezolvați orice problemă care implică suma unei progresii aritmetice, vă recomand să scrieți imediat cele două formule principale din acest subiect.
Formula pentru al n-lea termen:
Aceste formule vă vor spune imediat ce să căutați și în ce direcție să gândiți pentru a rezolva problema. Ajută.
Și acum sarcinile pentru o soluție independentă.
5. Aflați suma tuturor numerelor de două cifre care nu sunt divizibile cu trei.
Cool?) Sugestia este ascunsă în nota la problema 4. Ei bine, problema 3 va ajuta.
6. Progresia aritmetică este dată de condiția: a 1 = -5,5; a n+1 = a n +0,5. Aflați suma primilor 24 de termeni.
Neobișnuit?) Aceasta este o formulă recurentă. Puteți citi despre asta în lecția anterioară. Nu ignora legătura, astfel de probleme se găsesc adesea în Academia de Științe de Stat.
7. Vasya a făcut economii pentru vacanță. Cât de mult 4550 de ruble! Și am decis să-i ofer persoanei mele preferate (mie) câteva zile de fericire). Trăiește frumos fără a te nega nimic. Cheltuiește 500 de ruble în prima zi, iar în fiecare zi următoare cheltuiește cu 50 de ruble mai mult decât în cea anterioară! Până se epuizează banii. Câte zile de fericire a avut Vasya?
Este dificil?) Formula suplimentară de la sarcina 2 va ajuta.
Răspunsuri (în dezordine): 7, 3240, 6.
Daca va place acest site...
Apropo, mai am câteva site-uri interesante pentru tine.)
Puteți exersa rezolvarea exemplelor și puteți afla nivelul dvs. Testare cu verificare instantanee. Să învățăm - cu interes!)
Vă puteți familiariza cu funcțiile și derivatele.
Tip de lecție:învăţarea de materiale noi.
Obiectivele lecției:
- extinderea și aprofundarea înțelegerii de către elevi a problemelor rezolvate folosind progresia aritmetică; organizarea activităților de căutare ale elevilor la derivarea formulei pentru suma primilor n termeni ai unei progresii aritmetice;
- dezvoltarea capacității de a dobândi în mod independent noi cunoștințe și de a utiliza cunoștințele deja dobândite pentru a îndeplini o anumită sarcină;
- dezvoltarea dorintei si nevoii de generalizare a faptelor obtinute, dezvoltand independenta.
Sarcini:
- rezuma și sistematiza cunoștințele existente pe tema „Progresia aritmetică”;
- deduceți formule pentru calcularea sumei primilor n termeni ai unei progresii aritmetice;
- învață cum să aplici formulele obținute la rezolvarea diferitelor probleme;
- atrage atenţia elevilor asupra procedeului de aflare a valorii unei expresii numerice.
Echipament:
- fișe cu sarcini pentru lucrul în grupuri și perechi;
- lucrare de evaluare;
- prezentare„Progresie aritmetică”.
I. Actualizarea cunoștințelor de bază.
1. Munca independentă în perechi.
prima varianta:
Definiți progresia aritmetică. Scrieți o formulă de recurență care definește o progresie aritmetică. Vă rugăm să oferiți un exemplu de progresie aritmetică și să indicați diferența acesteia.
a 2-a varianta:
Scrieți formula pentru al n-lea termen al unei progresii aritmetice. Găsiți al 100-lea termen al progresiei aritmetice ( un n}: 2, 5, 8 …
În acest moment, doi elevi din spatele tablei pregătesc răspunsuri la aceleași întrebări.
Elevii evaluează munca partenerului lor verificându-le pe tablă. (Se predau foile cu răspunsuri.)
2. Momentul jocului.
Exercitiul 1.
Profesor. M-am gândit la o progresie aritmetică. Pune-mi doar două întrebări pentru ca după răspunsuri să poți numi rapid al 7-lea termen al acestei progresii. (1, 3, 5, 7, 9, 11, 13, 15…)
Întrebări de la studenți.
- Care este al șaselea termen al progresiei și care este diferența?
- Care este al optulea termen al progresiei și care este diferența?
Dacă nu mai există întrebări, atunci profesorul le poate stimula - o „interdicție” pe d (diferență), adică nu este permis să întrebați cu ce este egală diferența. Puteți pune întrebări: cu ce este egal al 6-lea termen al progresiei și cu ce este al 8-lea termen al progresiei?
Sarcina 2.
Pe tablă sunt scrise 20 de numere: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.
Profesorul stă cu spatele la tablă. Elevii sună numărul, iar profesorul sună imediat numărul în sine. Explicați cum pot face asta?
Profesorul își amintește formula pentru al n-lea trimestru a n = 3n – 2și, înlocuind valorile specificate n, găsește valorile corespunzătoare un n.
II. Stabilirea unei sarcini de învățare.
Îmi propun să rezolv o problemă străveche care datează din mileniul II î.Hr., găsită în papirusurile egiptene.
Sarcină:„Să vi se spună: împărțiți 10 măsuri de orz la 10 oameni, diferența dintre fiecare persoană și vecinul său este de 1/8 din măsură.”
- Cum este această problemă legată de progresia aritmetică a subiectului? (Fiecare persoană următoare primește 1/8 din măsură în plus, ceea ce înseamnă că diferența este d=1/8, 10 persoane, ceea ce înseamnă n=10.)
- Ce crezi că înseamnă numărul 10 măsuri? (Suma tuturor termenilor progresiei.)
- Ce altceva trebuie să știți pentru a face ușor și simplu împărțirea orzului în funcție de condițiile problemei? (Primul termen de progresie.)
Obiectivul lecției– obținerea dependenței sumei termenilor progresiei de numărul lor, primul termen și diferența și verificarea dacă problema a fost rezolvată corect în antichitate.
Înainte de a deduce formula, să ne uităm la modul în care egiptenii antici au rezolvat problema.
Și au rezolvat-o astfel:
1) 10 măsuri: 10 = 1 măsură – cotă medie;
2) 1 măsură ∙ = 2 măsuri – dublată in medie acțiune.
Dublat in medie cota este suma acțiunilor persoanei a 5-a și a 6-a.
3) 2 masuri – 1/8 masuri = 1 7/8 masuri – dublu fata de persoana a cincea.
4) 1 7/8: 2 = 5/16 – fracțiune de cincime; și așa mai departe, puteți găsi cota fiecărei persoane anterioare și ulterioare.
Obținem secvența:
III. Rezolvarea problemei.
1. Lucrați în grupuri
Grupa I: Aflați suma a 20 de numere naturale consecutive: S 20 =(20+1)∙10 =210.
În general ![]()
grupa II: Aflați suma numerelor naturale de la 1 la 100 (Legenda lui Micul Gauss).
S 100 = (1+100)∙50 = 5050
Concluzie: ![]()
grupa III: Aflați suma numerelor naturale de la 1 la 21.
Rezolvare: 1+21=2+20=3+19=4+18…
![]()
Concluzie: ![]()
grupa IV: Aflați suma numerelor naturale de la 1 la 101.
![]()
Concluzie: ![]()
Această metodă de rezolvare a problemelor luate în considerare se numește „Metoda Gauss”.
2. Fiecare grupă prezintă pe tablă soluția problemei.
3. Generalizarea soluțiilor propuse pentru o progresie aritmetică arbitrară:
a 1, a 2, a 3,..., a n-2, a n-1, a n.
S n =a 1 + a 2 + a 3 + a 4 +…+ a n-3 + a n-2 + a n-1 + a n.
Să găsim această sumă folosind un raționament similar:

4. Am rezolvat problema?(Da.)
IV. Înțelegerea și aplicarea primară a formulelor obținute la rezolvarea problemelor.
1. Verificarea soluției unei probleme vechi folosind formula.

2. Aplicarea formulei în rezolvarea diverselor probleme.
3. Exerciții de dezvoltare a capacității de a aplica formule la rezolvarea problemelor.
A) Nr. 613
Dat: ( a n) - progresie aritmetică;
(a n): 1, 2, 3, …, 1500
Găsi: S 1500
Soluţie: ![]() , a 1 = 1 și 1500 = 1500,
, a 1 = 1 și 1500 = 1500,
B) Având în vedere: ( a n) - progresie aritmetică;
(a n): 1, 2, 3, …
S n = 210
Găsi: n
Soluţie:

V. Munca independentă cu verificare reciprocă.
Denis a început să lucreze ca curier. În prima lună, salariul său a fost de 200 de ruble, în fiecare lună următoare a crescut cu 30 de ruble. Cât a câștigat în total într-un an?
Dat: ( a n) - progresie aritmetică;
a 1 = 200, d=30, n=12
Găsi: S 12
Soluţie:

Răspuns: Denis a primit 4380 de ruble pe an.
VI. Instruirea temelor pentru acasă.
- Secțiunea 4.3 – învață derivarea formulei.
- №№ 585, 623 .
- Creați o problemă care poate fi rezolvată folosind formula pentru suma primilor n termeni ai unei progresii aritmetice.
VII. Rezumând lecția.
1. Fișa de punctaj
2. Continuați propozițiile
- Astăzi la clasă am învățat...
- Formule invatate...
- Eu cred că …
3. Puteți găsi suma numerelor de la 1 la 500? Ce metodă veți folosi pentru a rezolva această problemă?
Bibliografie.
1. Algebră, clasa a IX-a. Manual pentru instituțiile de învățământ general. Ed. G.V. Dorofeeva. M.: „Iluminismul”, 2009.
Când studiezi algebra într-o școală secundară (clasa a IX-a), una dintre subiectele importante este studiul secvențelor numerice, care includ progresii - geometrice și aritmetice. În acest articol vom analiza o progresie aritmetică și exemple cu soluții.
Ce este o progresie aritmetică?
Pentru a înțelege acest lucru, este necesar să se definească progresia în cauză, precum și să se furnizeze formulele de bază care vor fi folosite ulterior în rezolvarea problemelor.
O progresie aritmetică sau algebrică este un set de numere raționale ordonate, fiecare termen diferit de cel anterior printr-o valoare constantă. Această valoare se numește diferență. Adică, cunoscând orice membru al unei serii ordonate de numere și diferența, puteți restabili întreaga progresie aritmetică.
Să dăm un exemplu. Următoarea succesiune de numere va fi o progresie aritmetică: 4, 8, 12, 16, ..., deoarece diferența în acest caz este 4 (8 - 4 = 12 - 8 = 16 - 12). Dar mulțimea numerelor 3, 5, 8, 12, 17 nu mai poate fi atribuită tipului de progresie luat în considerare, deoarece diferența pentru aceasta nu este o valoare constantă (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Formule importante
Să prezentăm acum formulele de bază care vor fi necesare pentru a rezolva probleme folosind progresia aritmetică. Să notăm cu simbolul a n al n-lea membru al secvenței, unde n este un număr întreg. Notăm diferența prin litera latină d. Atunci sunt valabile următoarele expresii:
- Pentru a determina valoarea celui de-al n-lea termen este potrivită următoarea formulă: a n = (n-1)*d+a 1 .
- Pentru a determina suma primilor n termeni: S n = (a n +a 1)*n/2.
Pentru a înțelege orice exemple de progresie aritmetică cu soluții în clasa a IX-a, este suficient să ne amintim aceste două formule, deoarece orice probleme de tipul luat în considerare se bazează pe utilizarea lor. De asemenea, trebuie să vă amintiți că diferența de progresie este determinată de formula: d = a n - a n-1.
Exemplul #1: găsirea unui membru necunoscut

Să dăm un exemplu simplu de progresie aritmetică și formulele care trebuie folosite pentru a o rezolva.
Să fie dată șirul 10, 8, 6, 4, ..., trebuie să găsiți cinci termeni în ea.
Din condițiile problemei rezultă deja că primii 4 termeni sunt cunoscuți. Al cincilea poate fi definit în două moduri:
- Să calculăm mai întâi diferența. Avem: d = 8 - 10 = -2. În mod similar, puteți lua oricare alți doi membri stând unul lângă celălalt. De exemplu, d = 4 - 6 = -2. Deoarece se știe că d = a n - a n-1, atunci d = a 5 - a 4, din care obținem: a 5 = a 4 + d. Inlocuim valorile cunoscute: a 5 = 4 + (-2) = 2.
- A doua metodă necesită, de asemenea, cunoașterea diferenței progresiei în cauză, așa că mai întâi trebuie să o determinați așa cum se arată mai sus (d = -2). Știind că primul termen a 1 = 10, folosim formula pentru numărul n al șirului. Avem: a n = (n - 1) * d + a 1 = (n - 1) * (-2) + 10 = 12 - 2*n. Înlocuind n = 5 în ultima expresie, obținem: a 5 = 12-2 * 5 = 2.
După cum puteți vedea, ambele soluții au dus la același rezultat. Rețineți că în acest exemplu diferența de progresie d este o valoare negativă. Astfel de secvențe se numesc descrescătoare, deoarece fiecare termen următor este mai mic decât cel anterior.
Exemplul #2: diferența de progresie
Acum să complicăm puțin sarcina, să dăm un exemplu despre cum
Se știe că la unii primul termen este egal cu 6, iar al 7-lea termen este egal cu 18. Este necesar să găsim diferența și să restabilim această secvență la al 7-lea termen.
Să folosim formula pentru a determina termenul necunoscut: a n = (n - 1) * d + a 1 . Să substituim datele cunoscute din condiție în ea, adică numerele a 1 și a 7, avem: 18 = 6 + 6 * d. Din această expresie puteți calcula cu ușurință diferența: d = (18 - 6) /6 = 2. Astfel, am răspuns la prima parte a problemei.
Pentru a restabili secvența la al 7-lea termen, ar trebui să utilizați definiția unei progresii algebrice, adică a 2 = a 1 + d, a 3 = a 2 + d și așa mai departe. Ca rezultat, restabilim întreaga secvență: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16, a 7 = 18.
Exemplul nr. 3: întocmirea unei progresii

Să complicăm și mai mult problema. Acum trebuie să răspundem la întrebarea cum să găsim o progresie aritmetică. Se poate da următorul exemplu: sunt date două numere, de exemplu - 4 și 5. Este necesar să se creeze o progresie algebrică astfel încât să mai fie plasați trei termeni între aceștia.
Înainte de a începe să rezolvați această problemă, trebuie să înțelegeți ce loc vor ocupa numerele date în progresia viitoare. Întrucât vor mai fi trei termeni între ei, atunci a 1 = -4 și a 5 = 5. După ce am stabilit acest lucru, trecem la problema, care este similară cu cea anterioară. Din nou, pentru al n-lea termen folosim formula, obținem: a 5 = a 1 + 4 * d. Din: d = (a 5 - a 1)/4 = (5 - (-4)) / 4 = 2,25. Ceea ce am obținut aici nu este o valoare întreagă a diferenței, ci este un număr rațional, deci formulele pentru progresia algebrică rămân aceleași.
Acum să adăugăm diferența găsită la un 1 și să restabilim termenii lipsă ai progresiei. Se obține: a 1 = - 4, a 2 = - 4 + 2.25 = - 1.75, a 3 = -1.75 + 2.25 = 0.5, a 4 = 0.5 + 2.25 = 2.75, a 5 = 2.75 + 2.25 = 5, care coincid cu condiţiile problemei.
Exemplul nr. 4: primul termen de progresie

Să continuăm să dăm exemple de progresie aritmetică cu soluții. În toate problemele anterioare, era cunoscut primul număr al progresiei algebrice. Acum să luăm în considerare o problemă de alt tip: să fie date două numere, unde a 15 = 50 și a 43 = 37. Este necesar să găsim cu ce număr începe această secvență.
Formulele folosite până acum presupun cunoașterea a 1 și d. În enunțul problemei, nu se știe nimic despre aceste numere. Cu toate acestea, vom nota expresii pentru fiecare termen despre care sunt disponibile informații: a 15 = a 1 + 14 * d și a 43 = a 1 + 42 * d. Am primit două ecuații în care există 2 mărimi necunoscute (a 1 și d). Aceasta înseamnă că problema se reduce la rezolvarea unui sistem de ecuații liniare.
Cel mai simplu mod de a rezolva acest sistem este de a exprima un 1 în fiecare ecuație și apoi de a compara expresiile rezultate. Prima ecuație: a 1 = a 15 - 14 * d = 50 - 14 * d; a doua ecuație: a 1 = a 43 - 42 * d = 37 - 42 * d. Echivalând aceste expresii, obținem: 50 - 14 * d = 37 - 42 * d, de unde diferența d = (37 - 50) / (42 - 14) = - 0,464 (se dau doar 3 zecimale).
Cunoscând d, puteți folosi oricare dintre cele 2 expresii de mai sus pentru un 1. De exemplu, mai întâi: a 1 = 50 - 14 * d = 50 - 14 * (- 0,464) = 56,496.
Dacă aveți îndoieli cu privire la rezultatul obținut, îl puteți verifica, de exemplu, determinați al 43-lea termen al progresiei, care este specificat în condiție. Se obține: a 43 = a 1 + 42 * d = 56,496 + 42 * (- 0,464) = 37,008. Mica eroare se datorează faptului că în calcule a fost folosită rotunjirea la miimi.
Exemplul nr. 5: suma
Acum să ne uităm la câteva exemple cu soluții pentru suma unei progresii aritmetice.
Să se dea o progresie numerică de următoarea formă: 1, 2, 3, 4, ...,. Cum se calculează suma a 100 dintre aceste numere?
Datorită dezvoltării tehnologiei informatice, este posibil să se rezolve această problemă, adică să se adauge toate numerele succesiv, ceea ce computerul va face imediat ce o persoană apasă tasta Enter. Problema poate fi însă rezolvată mental dacă acordați atenție faptului că seria de numere prezentată este o progresie algebrică, iar diferența ei este egală cu 1. Aplicând formula pentru suma, obținem: S n = n * (a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.
Este interesant de observat că această problemă se numește „gaussian” deoarece la începutul secolului al XVIII-lea celebrul german, încă în vârstă de doar 10 ani, a reușit să o rezolve în cap în câteva secunde. Băiatul nu știa formula pentru suma unei progresii algebrice, dar a observat că dacă aduni numerele de la sfârșitul șirului în perechi, obții întotdeauna același rezultat, adică 1 + 100 = 2 + 99. = 3 + 98 = ..., și deoarece aceste sume vor fi exact 50 (100 / 2), atunci pentru a obține răspunsul corect este suficient să înmulțiți 50 cu 101.

Exemplul nr. 6: suma termenilor de la n la m
Un alt exemplu tipic al sumei unei progresii aritmetice este următorul: având în vedere o serie de numere: 3, 7, 11, 15, ..., trebuie să aflați cu ce va fi suma termenilor săi de la 8 la 14. .
Problema este rezolvată în două moduri. Primul dintre ei implică găsirea de termeni necunoscuți de la 8 la 14 și apoi însumarea lor secvențială. Întrucât există puțini termeni, această metodă nu este destul de intensivă în muncă. Cu toate acestea, se propune rezolvarea acestei probleme folosind o a doua metodă, care este mai universală.
Ideea este de a obține o formulă pentru suma progresiei algebrice dintre termenii m și n, unde n > m sunt numere întregi. Pentru ambele cazuri, scriem două expresii pentru suma:
- S m = m * (a m + a 1) / 2.
- S n = n * (a n + a 1) / 2.
Deoarece n > m, este evident că a doua sumă o include pe prima. Ultima concluzie înseamnă că dacă luăm diferența dintre aceste sume și îi adăugăm termenul a m (în cazul luării diferenței se scade din suma S n), vom obține răspunsul necesar problemei. Avem: S mn = S n - S m + a m =n * (a 1 + a n) / 2 - m *(a 1 + a m)/2 + a m = a 1 * (n - m) / 2 + a n * n/2 + a m * (1- m/2). Este necesar să se înlocuiască formule pentru a n și a m în această expresie. Atunci obținem: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d *(3 * m - m 2 - 2) / 2.
Formula rezultată este oarecum greoaie, totuși, suma S mn depinde doar de n, m, a 1 și d. În cazul nostru, a 1 = 3, d = 4, n = 14, m = 8. Înlocuind aceste numere, obținem: S mn = 301.

După cum se poate observa din soluțiile de mai sus, toate problemele se bazează pe cunoașterea expresiei pentru al n-lea termen și a formulei pentru suma mulțimii primilor termeni. Înainte de a începe să rezolvați oricare dintre aceste probleme, este recomandat să citiți cu atenție starea, să înțelegeți clar ce trebuie să găsiți și abia apoi să continuați cu soluția.
Un alt sfat este să depuneți eforturi pentru simplitate, adică dacă puteți răspunde la o întrebare fără a utiliza calcule matematice complexe, atunci trebuie să faceți exact asta, deoarece în acest caz probabilitatea de a face o greșeală este mai mică. De exemplu, în exemplul unei progresii aritmetice cu soluția nr. 6, s-ar putea opri la formula S mn = n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m și împărțiți problema generală în subsarcini separate (în acest caz, găsiți mai întâi termenii a n și a m).
Dacă aveți îndoieli cu privire la rezultatul obținut, este recomandat să îl verificați, așa cum s-a făcut în unele dintre exemplele date. Am aflat cum să găsim o progresie aritmetică. Dacă îți dai seama, nu este atât de greu.
În această lecție vom obține o formulă pentru suma termenilor unei progresii aritmetice finite și vom rezolva unele probleme folosind această formulă.
Subiect: Progresii
Lecția: Formula pentru suma termenilor unei progresii aritmetice finite
1. Introducere
Luați în considerare problema: găsiți suma numerelor naturale de la 1 la 100 inclusiv.
Date: 1, 2, 3, …, 98, 99, 100.
Găsiți: S100=1+2+3 … +98 + 99 + 100.
Rezolvare: S100=(1+100)+(2+99)+(3+98)+…+(50+51)=101+101+101+…+101=101 x 50=5050.
Răspuns: 5050.
Sirul numerelor naturale 1, 2, 3, …, 98, 99, 100 este progresie aritmetică: a1=1, d=1.
Am găsit suma primelor sute de numere naturale, adică suma primului n termenii unei progresii aritmetice.
Soluția luată în considerare a fost propusă de marele matematician Carl Friedrich Gauss, care a trăit în secolul al XIX-lea. A rezolvat problema la vârsta de 5 ani.
Referință istorică: Johann Carl Friedrich Gauss (1777 - 1855) a fost un matematician, mecanic, fizician și astronom german. Considerat unul dintre cei mai mari matematicieni ai tuturor timpurilor, „Regele matematicienilor”. Laureat al medaliei Copley (1838), membru străin al Academiilor de Științe suedeză (1821) și rusă (1824) și al Societății Regale engleze. Potrivit legendei, un profesor de matematică din școală, pentru a ține copiii ocupați mult timp, le-a cerut să numere suma numerelor de la 1 la 100. Tânărul Gauss a observat că sumele perechi de la opuse sunt aceleași: 1+100=101 , 2+99=101 etc. etc. și a obținut instantaneu rezultatul: 101x50=5050.
2. Derivarea formulei pentru suma primilor n termeni ai unei progresii aritmetice
Să luăm în considerare o problemă similară pentru o progresie aritmetică arbitrară.
Aflați: suma primilor n termeni ai unei progresii aritmetice.
Să arătăm că toate expresiile dintre paranteze sunt egale între ele, și anume cu expresia . Fie d diferența unei progresii aritmetice. Apoi:
etc. Prin urmare, putem scrie:
De unde obținem formula pentru suma primilor n termeni ai unei progresii aritmetice:
![]() .
.
3. Rezolvarea problemelor folosind formula pentru suma primilor n termeni ai unei progresii aritmetice
1. Să rezolvăm problema sumei numerelor naturale de la 1 la 100 folosind formula pentru suma primilor n termeni ai unei progresii aritmetice:
Rezolvare: a1=1, d=1, n=100.
Formula generala:
![]() .
.
În cazul nostru: .
Răspuns: 5050.
Formula generala:
![]() . Să găsim al n-lea termen al progresiei aritmetice folosind formula:
. Să găsim al n-lea termen al progresiei aritmetice folosind formula: ![]() .
.
În cazul nostru: .
Pentru a găsi, trebuie mai întâi să găsiți.
Acest lucru se poate face folosind formula generală ![]() .Mai întâi aplicăm această formulă pentru a găsi diferența unei progresii aritmetice.
.Mai întâi aplicăm această formulă pentru a găsi diferența unei progresii aritmetice.
Acesta este ![]() . Mijloace .
. Mijloace .
Acum putem găsi.
Folosind formula pentru suma primilor n termeni ai unei progresii aritmetice
![]() , îl vom găsi.
, îl vom găsi.
4. Derivarea celei de-a doua formule pentru suma primilor n termeni ai unei progresii aritmetice
Să obținem a doua formulă pentru suma primilor n termeni ai unei progresii aritmetice și anume: demonstrăm că ![]() .
.
Dovada:
În formula pentru suma primilor n termeni ai unei progresii aritmetice ![]() să substituim expresia pentru , și anume
să substituim expresia pentru , și anume ![]() . Primim: , i.e.
. Primim: , i.e. ![]() . Q.E.D.
. Q.E.D.
Să analizăm formulele rezultate. Pentru calcule folosind prima formulă ![]() trebuie să cunoașteți primul termen, ultimul termen și n folosind a doua formulă
trebuie să cunoașteți primul termen, ultimul termen și n folosind a doua formulă ![]() - trebuie să cunoașteți primul termen, diferența și n.
- trebuie să cunoașteți primul termen, diferența și n.
Și în concluzie, observăm că în orice caz Sn este o funcție pătratică a lui n, deoarece ![]() .
.
5. Rezolvarea problemelor folosind a doua formulă pentru suma primilor n termeni ai unei progresii aritmetice
Formula generala:
![]() .
.
În cazul nostru:.
Răspuns: 403.
2. Aflați suma tuturor numerelor din două cifre care sunt multipli ai lui 4.
(12; 16; 20; …; 96) - un set de numere care îndeplinesc condițiile problemei.
Aceasta înseamnă că avem o progresie aritmetică.
n găsim din formula pentru:.
Acesta este ![]() . Mijloace .
. Mijloace .
Folosind a doua formulă pentru suma primilor n termeni ai unei progresii aritmetice
![]() , îl vom găsi.
, îl vom găsi.
Trebuie să găsiți suma tuturor termenilor de la 10 la 25 inclusiv.
O soluție este aceasta:
Prin urmare, .
6. Rezumatul lecției
Deci, am derivat formule pentru suma termenilor unei progresii aritmetice finite. Am folosit aceste formule pentru a rezolva unele probleme.
În lecția următoare ne vom familiariza cu proprietatea caracteristică a progresiei aritmetice.
1. Makarychev Yu. N. et al. Algebră clasa a IX-a (manual pentru liceu). - M.: Educație, 1992.
2. Makarychev Yu. N., Mindyuk N. G., Neshkov, K. I. Algebră pentru clasa a IX-a cu avansat. studiat Matematică.-M.: Mnemosyne, 2003.
3. Makarychev Yu. N., Mindyuk N. G. Capitole suplimentare pentru manualul școlii de algebră de clasa a 9-a. - M.: Prosveshchenie, 2002.
4. Galitsky M. L., Goldman A. M., Zvavich L. I. Culegere de probleme de algebră pentru clasele 8-9 (manual pentru elevii școlilor și claselor cu studiu aprofundat al matematicii) - M.: Prosveshchenie, 1996.
5. Mordkovich A.G. Algebră clasa a IX-a, manual pentru instituțiile de învățământ general. - M.: Mnemosyne, 2002.
6. Mordkovich A. G., Mishutina T. N., Tulchinskaya E. E. Algebra clasa a IX-a, cartea de probleme pentru instituțiile de învățământ. - M.: Mnemosyne, 2002.
7. Glazer G.I.Istoria matematicii la scoala. Clasele 7-8 (manual profesorului).- M.: Educaţie, 1983.
1. Secția colegiu. ru la matematică.
2. Portalul Științelor Naturii.
3. Exponenta. ru Site de matematică educațională.
1. Nr. 362, 371, 377, 382 (Makarychev Yu. N. et al. Algebra clasa a IX-a).
2. Nr. 12.96 (Galitsky M.L., Goldman A.M., Zvavich L.I. Culegere de probleme de algebră pentru clasele 8-9).